টাইম কমপ্লেক্সিটি কেন জানা দরকার?

আপনি কি কখনো ভেবে দেখেছেন, একই কাজ করার জন্য অনেক রকম কোড লেখা যায়? কিন্তু সব কোডই কি সমান ভালো? উত্তর হলো না!

কিছু কোড খুব দ্রুত কাজ করে, আবার কিছু কোড ধীরে ধীরে কাজ করে। বিশেষ করে যখন ডেটার পরিমাণ বাড়তে থাকে, তখন এই পার্থক্যটা আরো স্পষ্ট হয়ে ওঠে।

টাইম কমপ্লেক্সিটি হলো সেই পদ্ধতি যার মাধ্যমে আমরা বুঝতে পারি একটা অ্যালগরিদম কতটা সময় নেবে ইনপুটের আকারের উপর নির্ভর করে। সহজ কথায় বললে, এটা আমাদের বলে দেয় আমাদের কোড কতটা এফিশিয়েন্ট।

বিগ ও নোটেশন (Big O Notation) কি?

বিগ ও নোটেশন হলো টাইম কমপ্লেক্সিটি প্রকাশ করার একটা গাণিতিক পদ্ধতি। এটা আমাদের বলে দেয় ইনপুট বাড়লে সময় কতটা বাড়বে।

বিগ ও নোটেশনে আমরা সবসময় ওয়ার্স্ট কেস সিনারিও (Worst Case Scenario) বিবেচনা করি। মানে হলো সবচেয়ে খারাপ পরিস্থিতিতে কোড কতটা সময় নেবে।

Big-O Complexity: কোনটা কত দ্রুত?

একই কাজ করার জন্য অনেক রকম কোড লেখা যায়, কিন্তু সব কোডই কি সমান দ্রুত? না! Big-O Notation দিয়ে আপনি বুঝতে পারবেন আপনার কোড ইনপুট বাড়লে কতটা ধীর হবে।

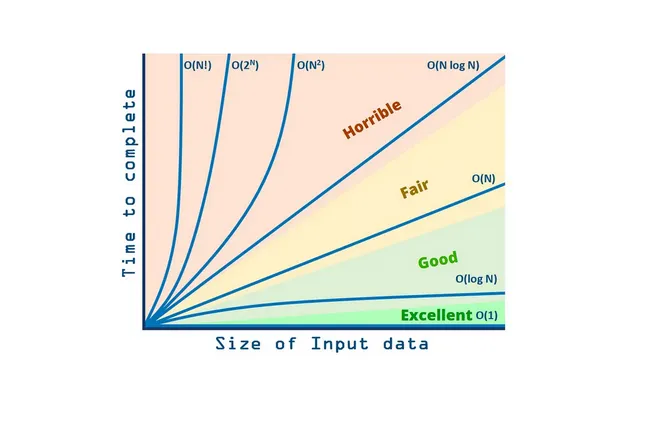
বাস্তব উদাহরণ (১০০০টা নাম খোঁজা):

• O(1): ১টা অপারেশন - সরাসরি ইন্ডেক্স দিয়ে (names[500])
• O(log N): ~১০টা অপারেশন - বাইনারি সার্চ (সর্টেড লিস্ট)
• O(N): ১০০০টা অপারেশন - সব নাম চেক করা
• O(N log N): ~১০,০০০টা অপারেশন - আগে সাজানো, তারপর খোঁজা
• O(N²): ১০,০০,০০০টা অপারেশন - প্রতিটি নামের সাথে সব নাম মিলানো
• O(2^N): অসীম অপারেশন - সব combination চেক করা
• O(N!): অসম্ভব বড় সংখ্যা - সব permutation তৈরি করা

সহজ ভাষায়:

• O(1): ইনপুট যতই বাড়ুক, সময় একই থাকে (সবচেয়ে ভালো)
• O(log N): ইনপুট দ্বিগুণ হলে সময় মাত্র একটু বাড়ে (খুব ভালো)
• O(N): ইনপুট দ্বিগুণ হলে সময়ও দ্বিগুণ হয় (ভালো)
• O(N log N): ইনপুট দ্বিগুণ হলে সময় একটু বেশি বাড়ে (মাঝারি)
• O(N²): ইনপুট দ্বিগুণ হলে সময় চারগুণ হয় (খারাপ)
• O(2^N): ইনপুট একটু বাড়লে সময় অনেক বেশি বাড়ে (খুব খারাপ)
• O(N!): ইনপুট একটু বাড়লে সময় অসম্ভব বাড়ে (ব্যবহারযোগ্য নয়)

দ্রুত ← O(1) > O(log N) > O(N) > O(N log N) > O(N²) > O(2^N) > O(N!) → ধীর

টাইম কমপ্লেক্সিটির প্রধান প্রকারভেদ

চলুন দেখি বিভিন্ন রকম নোটেশন, যেমন O(1), O(N), O(N²) এগুলো কী:

১. O(1) – অর্ডার অফ ওয়ান (কনস্ট্যান্ট টাইম)

এটা হলো কনস্ট্যান্ট টাইম কমপ্লেক্সিটি। মানে হলো ইনপুট সাইজ যতই বাড়ুক, সময়ের কমপ্লেক্সিটি বা সময়ের ব্যয় সবসময় একই থাকবে।

উপমা (চা বানানো)

ভাবুন, আপনি একবার বুদ্ধি করে এক গামলা চা বানিয়ে ফেললেন। এখন ১০ জন, ২০ জন বা ৫০ জন গেস্ট আসলেও চা বানানোর জন্য আর অতিরিক্ত সময় ব্যয় হবে না। সময় কনস্ট্যান্ট থাকবে।

কোড উদাহরণ (অ্যারে)

আপনি যদি অ্যারেতে সরাসরি ইন্ডেক্স ব্যবহার করে কোনো এলিমেন্টকে তুলে আনেন, তাহলে ইনপুট সাইজ যত বড়ই হোক, সময় একই লাগবে। কারণ আপনি ডাইরেক্টলি ইন্ডেক্স জানেন।

// O(1) - কনস্ট্যান্ট টাইম
function getFirstElement(arr) {
  return arr[0]; // সরাসরি প্রথম এলিমেন্ট নিয়ে আসা
}

const numbers = [1, 2, 3, 4, 5, 100, 1000];
console.log(getFirstElement(numbers)); // 1 - সবসময় একই সময় লাগে

উপমা (টেলিফোন ডাইরেক্টরি)

ভাবুন, ডাইরেক্টরিতে ইন্ডেক্সিং আছে। আপনি সরাসরি সেই পেজে (যেমন, ১১৯৯ নম্বর পেজ) চলে যেতে পারেন এবং নাম খুঁজে নিতে পারেন। এতে সময় কনস্ট্যান্ট থাকবে।

গ্রাফ

O(1) এর গ্রাফ একটা সমান্তরাল রেখা:

সময়
  ↑
  │  O(1) ────────────────────────────────
  │
  │
  └──────────────────────────────────────→ ইনপুট সাইজ

ইনপুট যতই বাড়ুক, সময় একই থাকে!

O(1) হলো সবচেয়ে এফিশিয়েন্ট কমপ্লেক্সিটি।

২. O(N) – অর্ডার অফ এন (লিনিয়ার টাইম)

এক্ষেত্রে ইনপুট সাইজ (N) যত বাড়ে, টাইম কমপ্লেক্সিটিও ঠিক সেই অনুপাতে বাড়ে। মানে ইনপুট বাড়া বা কমার সাথে সাথে সময়ের বাড়া বা কমার অনুপাত একই থাকে।

উপমা (চা বানানো)

ভাবুন, প্রত্যেক নতুন গেস্টের জন্য এক কাপ করে চা বানাতে হচ্ছে। গেস্টের সংখ্যা বাড়ার সঙ্গে সঙ্গে চা বানানোর মোট সময় সমানুপাতে বাড়তে থাকে।

কোড উদাহরণ (ফরলুপ)

একটা অ্যারের প্রত্যেকটা এলিমেন্টের ওপর দিয়ে ফরলুপ চালিয়ে ইটারেট করা। অ্যারেতে এলিমেন্ট সংখ্যা বাড়লে লুপ ঘোরার সংখ্যাও বাড়বে, ফলে সময় বাড়বে।

// O(N) - লিনিয়ার টাইম
function findElement(arr, target) {
  for (let i = 0; i < arr.length; i++) {
    if (arr[i] === target) {
      return i; // এলিমেন্ট পাওয়া গেছে
    }
  }
  return -1; // পাওয়া যায়নি
}

const numbers = [1, 2, 3, 4, 5];
console.log(findElement(numbers, 3)); // 2 - ৩টি এলিমেন্ট চেক করতে হয়েছে

উপমা (টেলিফোন ডাইরেক্টরি)

ইন্ডেক্স ছাড়া প্রত্যেকটা পেজ উল্টে উল্টে নাম খোঁজা। যদি ১০০০ পেজ থাকে, তাহলে সবচেয়ে খারাপ ক্ষেত্রে ১০০০ পেজ দেখতে হবে।

গ্রাফ

O(N) এর গ্রাফ একটা সোজা লাইন:

সময়
  ↑
  │     O(N) ────────────────
  │    /
  │   /
  │  /
  │ /
  └────────────────────────→ ইনপুট সাইজ

৩. O(N²) – অর্ডার অফ এন স্কোয়ার

এটা কমপ্লেক্সিটি আসে যখন কোডে নেস্টেড লুপ (একটা ফরলুপের মধ্যে আরেকটা ফরলুপ) থাকে।

• বাইরের লুপের একবার ঘোরার জন্য ভিতরের লুপটা তার সম্পূর্ণ টার্ন কমপ্লিট করে।
• যদি N-এর ভ্যালু 5 হয়, লুপটা মোট 5 × 5 = 25 বার ঘুরবে।
• ইনপুট সাইজ বাড়লে সময় শার্পলি রাইজ করে এবং গ্রাফটা লিনিয়ার স্ট্রেট লাইন হয় না।
• O(N²) আসে যখন আমাদের এন ইনটু এন (N×N) বার ঘুরতে হয়।

কোড উদাহরণ

// O(N²) - কোয়াড্রাটিক টাইম
function printPairs(arr) {
  for (let i = 0; i < arr.length; i++) {
    for (let j = 0; j < arr.length; j++) {
      console.log(arr[i], arr[j]); // সব সম্ভাব্য জোড়া প্রিন্ট করা
    }
  }
}

const numbers = [1, 2, 3];
printPairs(numbers);
// আউটপুট: (1,1), (1,2), (1,3), (2,1), (2,2), (2,3), (3,1), (3,2), (3,3)
// মোট 9 বার (3 × 3)

উপমা

ধরুন, আপনি একটি ক্লাসে আছেন যেখানে ১০ জন ছাত্র আছে। যদি প্রত্যেক ছাত্রের সাথে প্রত্যেক ছাত্রের হ্যান্ডশেক করতে হয়, তাহলে মোট হ্যান্ডশেক হবে 10 × 10 = 100 বার। যদি ছাত্র সংখ্যা ২০ হয়, তাহলে 20 × 20 = 400 বার।

গ্রাফ

O(N²) এর গ্রাফ একটা কার্ভ যা দ্রুত বাড়ে:

সময়
  ↑
  │                    O(N²) ────────
  │                  /
  │                /
  │              /
  │            /
  │          /
  │        /
  └──────────────────────────────────→ ইনপুট সাইজ

৪. O(log N) – অর্ডার অফ লগ এন (লগারিদমিক টাইম)

এ ধরনের কমপ্লেক্সিটি এমন অ্যালগরিদমে দেখা যায় যেখানে সমস্যাকে সমানভাবে বার বার দুই ভাগে ভেঙে সমাধান খোঁজা হয় (হাফ হাফ করে স্প্লিট)।

উদাহরণ: বাইনারি সার্চ (Binary Search)

যদি 16টা এলিমেন্ট থাকে, তাহলে লগারিদমের হিসাব অনুযায়ী সর্বোচ্চ 4টা স্টেপে (log₂16 = 4) এলিমেন্টটা খুঁজে পাওয়া সম্ভব।

কোড উদাহরণ

// O(log N) - লগারিদমিক টাইম
function binarySearch(arr, target) {
  let left = 0;
  let right = arr.length - 1;

  while (left <= right) {
    let mid = Math.floor((left + right) / 2); // মাঝখানে ভাগ করা

    if (arr[mid] === target) {
      return mid; // পাওয়া গেছে
    } else if (arr[mid] < target) {
      left = mid + 1; // ডান দিকে যাওয়া
    } else {
      right = mid - 1; // বাম দিকে যাওয়া
    }
  }

  return -1; // পাওয়া যায়নি
}

const sortedNumbers = [1, 3, 5, 7, 9, 11, 13, 15];
console.log(binarySearch(sortedNumbers, 7)); // 3
// মাত্র 3টি স্টেপে 7 খুঁজে পাওয়া গেছে

উপমা (টেলিফোন ডাইরেক্টরি)

ভাবুন, আপনি একটা টেলিফোন ডাইরেক্টরিতে নাম খুঁজছেন যা A-Z অর্ডারে সাজানো আছে। আপনি মাঝখান দিয়ে খুলবেন, ধরুন M-এ গেলেন। যদি আপনার নাম M-এর পরে থাকে, তাহলে M-এর পরের অংশে খুঁজবেন। এভাবে প্রতিবার অর্ধেক করে কমিয়ে আপনি দ্রুত নাম খুঁজে পাবেন।

গ্রাফ

O(log N) এর গ্রাফ খুব ধীরে ধীরে বাড়ে:

সময়
  ↑
  │        O(log N) ────────────
  │      /
  │    /
  │  /
  │/
  └────────────────────────────→ ইনপুট সাইজ

O(log N) O(N) এর তুলনায় ভালো কমপ্লেক্সিটি।

৫. O(2^N) – এক্সপোনেনশিয়াল টাইম

এটা কমপ্লেক্সিটি আসে রিকারশন (Recursion) এর ক্ষেত্রে, যেমন ফিবোনাচি সিরিজ ফাংশনে। এখানে প্রতিটি কল থেকে নতুন দুটো করে কলের সৃষ্টি হয়, ফলে সময়ের বৃদ্ধি হয় এক্সপ্লোসিভলি।

এটা O(N²) এর থেকে ভিন্ন। N² মানে N-এর মাথায় টু, আর O(2^N) মানে টু-এর মাথায় N।

কোড উদাহরণ

// O(2^N) - এক্সপোনেনশিয়াল টাইম (খুব ধীর!)
function fibonacci(n) {
  if (n <= 1) {
    return n;
  }
  return fibonacci(n - 1) + fibonacci(n - 2);
  // প্রতিটি কল থেকে দুটো নতুন কল
}

console.log(fibonacci(5)); // 5
// কিন্তু fibonacci(40) চালালে অনেক সময় লাগবে!

কেন এত ধীর?

যদি fibonacci(5) কল করি:

• fibonacci(5) → fibonacci(4) + fibonacci(3)
• fibonacci(4) → fibonacci(3) + fibonacci(2)
• fibonacci(3) → fibonacci(2) + fibonacci(1)
• …এভাবে গাছের মতো ছড়িয়ে পড়ে

N = 40 হলে প্রায় 2^40 ≈ 1 ট্রিলিয়ন অপারেশন হতে পারে! ভাবুন কত ধীর!

গ্রাফ

O(2^N) এর গ্রাফ এক্সপোনেনশিয়ালি বাড়ে:

সময়
  ↑
  │                                    O(2^N) ────────
  │                                  /
  │                                /
  │                              /
  │                            /
  │                          /
  │                        /
  │                      /
  │                    /
  │                  /
  │                /
  └──────────────────────────────────────────────→ ইনপুট সাইজ

এটা খুবই বিপজ্জনক! ছোট ইনপুটেও সময় অনেক বেশি লাগে।

৬. O(N log N) – অর্ডার অফ এন লগ এন

এটা কমপ্লেক্সিটি দেখা যায় অনেক সর্টিং অ্যালগরিদম এ, যেমন Merge Sort, Quick Sort, Heap Sort।

কোড উদাহরণ

// O(N log N) - Merge Sort এর মতো
function mergeSort(arr) {
  if (arr.length <= 1) return arr;

  const mid = Math.floor(arr.length / 2);
  const left = mergeSort(arr.slice(0, mid)); // O(log N) levels
  const right = mergeSort(arr.slice(mid)); // O(log N) levels

  return merge(left, right); // O(N) per level
}

function merge(left, right) {
  const result = [];
  let i = 0,
    j = 0;

  while (i < left.length && j < right.length) {
    if (left[i] < right[j]) {
      result.push(left[i++]);
    } else {
      result.push(right[j++]);
    }
  }

  return result.concat(left.slice(i)).concat(right.slice(j));
}

কেন O(N log N)?

• Merge Sort প্রতিবার অ্যারেকে দুই ভাগে ভাগ করে (O(log N) levels)
• প্রতিটি level এ O(N) কাজ করে
• তাই মোট: O(N) × O(log N) = O(N log N)

গ্রাফ

O(N log N) এর গ্রাফ O(N) এর চেয়ে বেশি কিন্তু O(N²) এর চেয়ে কম:

সময়
  ↑
  │                    O(N log N) ────────
  │                  /
  │                /
  │              /
  │            /
  │          /
  │        /
  └──────────────────────────────────→ ইনপুট সাইজ

উপমা

ভাবুন, আপনি একটা বইয়ের সব পেজ সাজাতে চান। Merge Sort এর মতো করে:

• প্রথমে বইকে দুই ভাগে ভাগ করুন
• প্রতিটি ভাগ আবার দুই ভাগে ভাগ করুন
• এভাবে যতক্ষণ না এক পেজ থাকে
• তারপর আবার একসাথে জোড়া দিন

এতে সময় লাগে O(N log N)।

৭. O(N!) – অর্ডার অফ এন ফ্যাক্টোরিয়াল

এটা সবচেয়ে খারাপ কমপ্লেক্সিটি! দেখা যায় permutation বা combination এর সমস্যায়।

কোড উদাহরণ

// O(N!) - সব সম্ভাব্য permutation তৈরি করা
function generatePermutations(arr) {
  if (arr.length <= 1) return [arr];

  const result = [];
  for (let i = 0; i < arr.length; i++) {
    const rest = [...arr.slice(0, i), ...arr.slice(i + 1)];
    const perms = generatePermutations(rest); // (N-1)! recursive calls

    for (let perm of perms) {
      result.push([arr[i], ...perm]);
    }
  }

  return result;
}

// N = 5 হলে 5! = 120 permutation
// N = 10 হলে 10! = 3,628,800 permutation

কেন এত ধীর?

• N = 5 হলে: 5! = 120 অপারেশন
• N = 10 হলে: 10! = 3,628,800 অপারেশন
• N = 20 হলে: 20! = 2,432,902,008,176,640,000 অপারেশন!

এটা ব্যবহারযোগ্য নয়!

গ্রাফ

O(N!) এর গ্রাফ সবচেয়ে খারাপ:

সময়
  ↑
  │                                    O(N!) ────────
  │                                  /
  │                                /
  │                              /
  │                            /
  │                          /
  │                        /
  │                      /
  │                    /
  │                  /
  │                /
  └──────────────────────────────────────────────→ ইনপুট সাইজ

উপমা

ভাবুন, আপনি ১০ জন মানুষকে একটা সারিতে সাজাতে চান। সব সম্ভাব্য সাজানো দেখতে হলে:

• প্রথম স্থানে ১০ জনের যেকোনো একজন
• দ্বিতীয় স্থানে বাকি ৯ জনের যেকোনো একজন
• এভাবে…

মোট সম্ভাবনা: 10! = 3,628,800

এটা খুবই ধীর!

টাইম কমপ্লেক্সিটির কার্যকারিতা অনুযায়ী ক্রম (Best to Worst)

আমাদের সবসময় অর্ডার অফ ওয়ান (O(1)) ই প্রেফার করা উচিত। এফিশিয়েন্সির ক্রমটা হলো:

O(1) > O(log N) > O(N) > O(N log N) > O(N²) > O(2^N) > O(N!)

তুলনামূলক উদাহরণ

ভাবুন, আপনার কাছে 1,000,000 (10 লাখ) এলিমেন্ট আছে:

• O(1): 1 অপারেশন (সবচেয়ে দ্রুত)
• O(log N): ~20 অপারেশন (খুব দ্রুত)
• O(N): 1,000,000 অপারেশন (মাঝারি)
• O(N log N): ~20,000,000 অপারেশন (মাঝারি)
• O(N²): 1,000,000,000,000 অপারেশন (খুব ধীর)
• O(2^N): প্রায় অসীম অপারেশন (ব্যবহারযোগ্য নয়)
• O(N!): অসম্ভব বড় সংখ্যা (ব্যবহারযোগ্য নয়)

স্পেস কমপ্লেক্সিটি (Space Complexity)

স্পেস কমপ্লেক্সিটি হলো কোড রান করার জন্য কতটা এক্সট্রা মেমোরি লাগে।

O(1) স্পেস কমপ্লেক্সিটি

যখন কোডটা সোর্স অ্যারে পরিবর্তন করে বা ইনপুট সাইজ বাড়লেও এক্সট্রা কোনো অ্যারে বা স্পেস তৈরি করে না, তখন স্পেস কনস্ট্যান্ট থাকে।

// O(1) স্পেস - এক্সট্রা মেমোরি লাগে না
function findMax(arr) {
  let max = arr[0];
  for (let i = 1; i < arr.length; i++) {
    if (arr[i] > max) {
      max = arr[i];
    }
  }
  return max;
}

O(N) স্পেস কমপ্লেক্সিটি

যখন ইনপুট সাইজের অনুপাতে (N এলিমেন্টের জন্য N স্পেস) নতুন অ্যারে তৈরি হয় বা অতিরিক্ত মেমোরি লাগে।

// O(N) স্পেস - নতুন অ্যারে তৈরি হচ্ছে
function doubleArray(arr) {
  let newArr = [];
  for (let i = 0; i < arr.length; i++) {
    newArr.push(arr[i] * 2);
  }
  return newArr; // N সাইজের নতুন অ্যারে
}

কোড লেখার সময় আমাদের টাইম কমপ্লেক্সিটির পাশাপাশি স্পেস কমপ্লেক্সিটি নিয়েও ভাবতে হবে। আমরা অতিরিক্ত ভেরিয়েবল বা অ্যারে ক্রিয়েট করছি কিনা সেটা দেখতে হবে।

বিগ ও নোটেশন বার করার সাধারণ নিয়মাবলী

একটা কোডের বিগ ও ভ্যালু নির্ণয় করার জন্য এই নিয়মগুলো মনে রাখুন:

১. লুপের সংখ্যা

লুপ কয়বার চলছে দেখুন। এন এলিমেন্টের জন্য লুপ এন বার চললে অর্ডার অফ এন (O(N))।

// O(N) - একটি লুপ
for (let i = 0; i < n; i++) {
  // কাজ
}

২. নেস্টেড লুপ

নেস্টেড লুপ থাকলে সেগুলোকে মাল্টিপ্লাই করুন (N × N = O(N²) বা N × N × N = O(N³))।

// O(N²) - দুটি নেস্টেড লুপ
for (let i = 0; i < n; i++) {
  for (let j = 0; j < n; j++) {
    // কাজ
  }
}

// O(N³) - তিনটি নেস্টেড লুপ
for (let i = 0; i < n; i++) {
  for (let j = 0; j < n; j++) {
    for (let k = 0; k < n; k++) {
      // কাজ
    }
  }
}

৩. কনস্ট্যান্ট বাদ দিন

যদি একাধিক লুপ নেস্টেড না হয়ে পরপর থাকে (O(N) + O(N) = O(2N)), তবে কনস্ট্যান্ট (যেমন 2) বাদ দিন। সেক্ষেত্রে কমপ্লেক্সিটি O(N) ই হয়।

// O(N) + O(N) = O(2N) = O(N) - কনস্ট্যান্ট বাদ যায়
for (let i = 0; i < n; i++) {
  // কাজ ১
}
for (let i = 0; i < n; i++) {
  // কাজ ২
}

৪. ওয়ার্স্ট কেস সিনারিও

সবসময় ওয়ার্স্ট কেস সিনারিও (Worst Case Scenario) বিবেচনা করতে হবে। উদাহরণস্বরূপ, বাইনারি সার্চের ক্ষেত্রে ওয়ার্স্ট কেস সিনারিও বিবেচনা করেই অর্ডার অফ লগ এন নির্ধারণ করা হয়।

// O(log N) - সবচেয়ে খারাপ ক্ষেত্রে log N স্টেপ লাগে
function binarySearch(arr, target) {
  // ... কোড
}

কেন কমপ্লেক্সিটি গুরুত্বপূর্ণ?

১. স্কেলেবিলিটি (Scalability)

যখন আপনার অ্যাপ্লিকেশন বড় হবে এবং ডেটা বাড়বে, তখন O(N²) বা O(2^N) অ্যালগরিদম ব্যবহারযোগ্য হবে না। O(N) বা O(log N) ব্যবহার করলে অ্যাপ্লিকেশন দ্রুত কাজ করবে।

২. ইউজার এক্সপিরিয়েন্স

কেউ আপনার ওয়েবসাইটে সার্চ করলে, যদি সার্চ O(N²) হয়, তাহলে অনেক সময় লাগবে এবং ইউজার বিরক্ত হবে। কিন্তু O(log N) হলে দ্রুত ফলাফল পাবে।

৩. সার্ভার কস্ট

ধীর অ্যালগরিদম বেশি CPU এবং মেমোরি ব্যবহার করে, যা সার্ভার কস্ট বাড়ায়। এফিশিয়েন্ট অ্যালগরিদম ব্যবহার করলে কম রিসোর্স লাগে।

বাস্তব জীবনের উদাহরণ

O(1) - ডিকশনারি/হ্যাশম্যাপ

const dictionary = {
  apple: "আপেল",
  banana: "কলা",
  orange: "কমলা",
};

// O(1) - সরাসরি key দিয়ে value পাওয়া
console.log(dictionary["apple"]); // "আপেল"

O(N) - লিস্টে সার্চ করা

// O(N) - লিস্টের সব এলিমেন্ট চেক করা
function findInList(list, item) {
  for (let i = 0; i < list.length; i++) {
    if (list[i] === item) {
      return true;
    }
  }
  return false;
}

O(log N) - বাইনারি সার্চ

// O(log N) - সর্টেড অ্যারেতে দ্রুত খোঁজা
function binarySearch(sortedArray, target) {
  // ... উপরের কোড
}

O(N²) - সব সম্ভাব্য জোড়া

// O(N²) - সব সম্ভাব্য জোড়া তৈরি করা
function findAllPairs(arr) {
  const pairs = [];
  for (let i = 0; i < arr.length; i++) {
    for (let j = i + 1; j < arr.length; j++) {
      pairs.push([arr[i], arr[j]]);
    }
  }
  return pairs;
}

শেষ কথা

বিগ ও নোটেশন আমাদের টাইম এবং স্পেস কমপ্লেক্সিটি, দুটোই পরিমাপ করতে সাহায্য করে এবং কোডকে এফিশিয়েন্টলি কাজ করাতে সাহায্য করে।

মনে রাখবেন, কোড শুধু কাজ করলেই হবে না, এটাকে দক্ষতা সহকারে কাজ করতে হবে।

যখনই আপনি একটা নতুন অ্যালগরিদম লিখবেন, নিজেকে জিজ্ঞাসা করুন:

• এই কোডের টাইম কমপ্লেক্সিটি কত?
• ইনপুট বাড়লে কতটা ধীর হবে?
• আরো ভালো উপায় আছে কিনা?

এই প্রশ্নগুলোর উত্তর জানলে আপনি একজন ভালো প্রোগ্রামার হয়ে উঠবেন!